Data-Driven Science: A Paradigm Shift or a Misnomer?

The Philosophy of Science in the Era of Data-Driven Discovery

As the practice of science has evolved throughout history it has converged on a set of principles and practices that enable it to both predict and explain natural phenomena. Protoscience as it existed in ancient Greece was largely about using observations to derive universal principles through syllogistic reasoning, and explaining observations through those universals. With the dawn of the scientific revolution in the 16th century science developed quantitative and mechanistic theoretical frameworks that could be used to predict diverse phenomena. This paradigm also involved lengthy calculations, for instance the differential equations solved by Urbain Le Verrier to predict the existence and position of Neptune, however it was the advent of computers that truly enabled numerical simulation to become a core feature of scientific practice. This drove the analysis of large datasets and the discovery of new techniques in numerical algorithms, leading to advances in fields like computational fluid dynamics and computational chemistry. More recently, advances in statistical modelling and deep learning have enabled the production of predictive models from terabytes of raw data, even in the absence of theoretical understanding.

This evolution of scientific practice was described by computer scientist Jim Gray in a 2007 talk on 'A Transformed Scientific Method', calling the ascendant paradigm of data-driven research the 'fourth paradigm' of science. However, because the notion of a scientific paradigm has already been developed by Kuhn in The Structure of Scientific Revolutions (e.g. the Ptolemaic and Copernican paradigms of astronomy) I will henceforth be referring to Gray's paradigms as metaparadigms, as they describe different methodological and epistemic approaches to science itself, rather than competing scientific theories.Data-Driven Science: A Paradigm Shift or a Misnomer?

The progression of metaparadigms certainly makes sense, given the historical development of our scientific theories and technologies. However it is also built on an underlying assumption that every successive metaparadigm is, in fact, 'science'. Every metaparadigm represents a research methodology, but not all research methodologies are isomorphic to science, and it is not a given that the fourth metaparadigm can be described as a science in the same way that the second metaparadigm can. I have elsewhere described the difference between science - the production of explanatory theories of causality - and engineering - the production of heuristic models for control. This definition will undergird the argument that follows.

It is worth noting that Jim Gray was a computer scientist who made seminal contributions to the development of database systems. His talk was given in 2007, before the explosion in neural network-based AI systems that began in the 2010s. Big data was emerging as a concept but hadn't yet been realized in industrial or scientific applications. Thus, the fourth metaparadigm as Gray presents it is largely about how to overcome the challenges in implementing systems to collect, organize, analyze, and share data. In other words, the talk focuses on the challenges of supporting a data-driven metaparadigm from the perspective of software engineering, as opposed to that of a scientist working on specific problems within the metaparadigm, or a philosopher interrogating the epistemological basis of such a system.

Now, almost two decades into this metaparadigm, the tools and workflows associated with it have advanced considerably, and there is even a book exploring its ramifications from the perspective of various fields. However, as I have presented it so far, I cannot consider the fourth metaparadigm to be a truly novel means of conducting research: rather it is simply a sociological development, bringing the tools of science up to date with modern methods of data collection, sharing, and analysis. Where it really becomes something new is in deep learning-driven research. That perspective is well captured by the essay A Future History of Biomedical Progress by Adam Green, writing for Markov Bio. The central theme of the essay is this: "[future biomedical progress] will require discarding the reductionist, human-legibility-centric research ethos underlying current biomedical research, which has generated the remarkable basic biology progress we have seen, in favor of a purely control-centric ethos based on machine learning." As we can see, this lines up directly with my definitions of science and engineering.

As such, my central claim is that any research paradigm operating in such a way is fundamentally pursuing engineering rather than science. The point is not to argue that data-driven research methods are not relevant or useful, but that the distinction between engineering and science is an important epistemological dimension that must be considered when evaluating the potential and results of different research methods. The most important difference is given in the essay: "Just as large models trained on human language data learn to approximate the general function “talk (and, eventually, reason) like a human”, large models trained on biological data will learn to approximate the general function “biomedical dynamics”—without needing to simulate the true causal structure of the underlying biological system."

This is a crucial point because understanding the causal structure of scientific phenomena is an indispensable part of sustainable progress in science. As I have argued, dispensing with the goal of actually understanding causal mechanics in favour of instrumental modelling often leads to a failure to generalize our understanding to unseen situations or to novel paradigms. Causal modelling, as in our understanding of gene transcription and translation and related processes, has lead to the great advances we have seen in our understanding of biological systems over the past half-century. However, Green makes the case that attempting to incorporate this causal framework into machine learning models could end up hindering their progress. He notes multiple examples of the "bitter lesson" in machine learning - that attempting to build knowledge into AI models may improve performance in the short term, but in the long run further progress is achieved through simply scaling data and computation in the absence of any feature engineering.¹ Thus he says:

Throwing out the scientific abstractions that have been painstakingly learned through decades of experimental research seems like a bad idea—we probably shouldn’t ignore the concept of genes and start naively using raw, unmapped sequencing reads. But, on the other hand, once we have enough data, perhaps these abstractions will hinder dynamics model performance—raw reads contain information (e.g., about transcriptional regulation) that isn’t captured by mapped gene counts. These abstractions may have been necessary to reason our way through building tools like sequencing, but now that they’ve been built, we must evolve beyond these abstractions.

It is entirely possible that research progress in a deep learning metaparadigm will eventually require dispensing with the theoretical causal constructs that have scaffolded the advances up until now. However, even if this is not the case, it is nonetheless very likely the case that AI models will not be able to supply us with new constructs. Understanding the emergent behaviour of how AI systems work internally (i.e. the science of AI models, as opposed to their engineering) is still in its infancy. AI systems are still largely treated as inscrutable black boxes that spit out useful answers. Without a revolution in understanding the inner workings of deep learning models, it is unlikely that we would be able to extract any useful insights from a model trained in some scientific domain. And, of course, such a model would not be able to introspect itself and tell us, either.

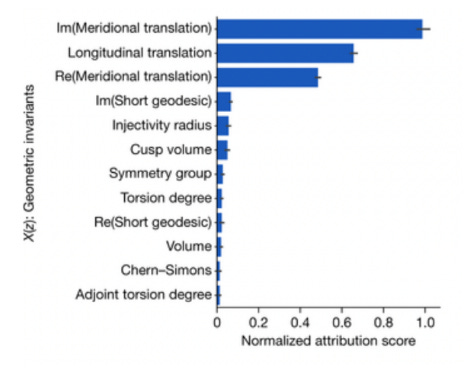
To demonstrate why this is a problem, we can turn to an example from experimental mathematics. Knot theory is a branch of mathematics that studies closed loops embedded in 3D space. Knots are considered the same when they can be transformed into one another without cutting or intersecting themselves. Each distinct knot possesses a number of invariant properties, like the minimum number of crossings, or polynomials derived from the knot diagram. Researchers were interested in whether there was a relationship between two kinds of invariants, called hyperbolic invariants and the knot signature. They trained an ML model on over two million knots, and discovered that the neural network was able to predict knot signature from the hyperbolic invariants with high accuracy. It had discovered an empirical relationship, however it could not by itself inform the researchers as to what the underlying structure was. For the same reason, the network could not be used as a foundational result to build additional theorems in pure mathematics. Through performing a saliency analysis on the model, the researchers were able to discover that only three of the hyperbolic invariants were strongly associated with changes in the final output.² Based on this new information, they were able to form a conjecture and eventually prove the relationship between the hyperbolic invariants and the knot signature.

While this case serves as an example of the potential benefits of using machine learning to discover new math, it highlights a key limitation: such models, without additional interpretability, cannot serve as a foundation for further developments in pure mathematics. It was only because the model was legible (in some small way) that it was able to aid in the advancement of mathematics. It should also be noted that saliency analysis on a model with only 12 input parameters is much easier than the kind of model introspection that would be required by most scientific enterprise. Although deep-learning introspection is still in an inchoate form, it may be that it is fundamentally bounded in its practical application, even in the best case. Since AI models represent a statistical approximation of a particular data set (which is itself a partial sample of a space of possibilities), rather than the actual underlying dynamics, it is not clear to what extent making a model more interpretable would actually lead to advances in the theoretical understanding of the problem it is approximating. Therefore, while this is a compelling early example of how machine learning could be applied to science or mathematics, there is still much work to be done before this tool could be applied more generally.

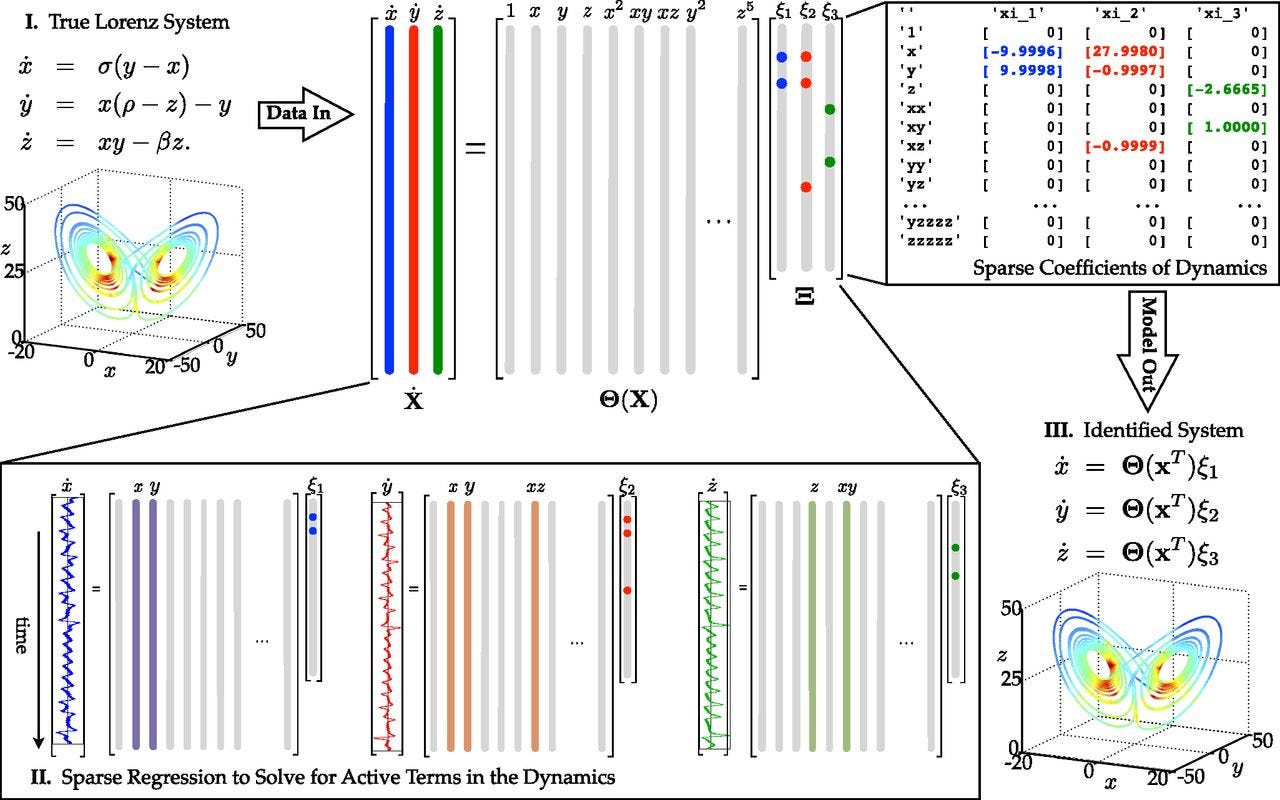
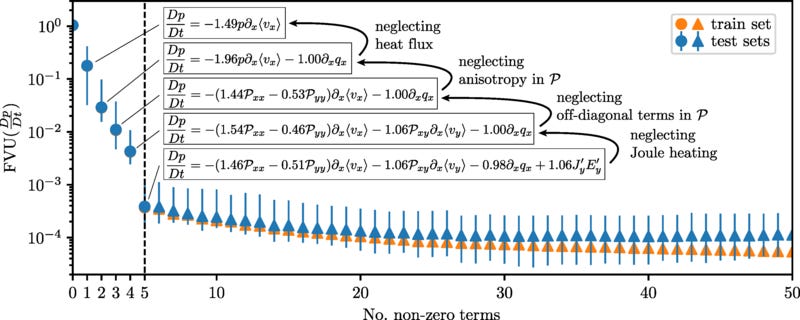
The best progress towards a truly scientific machine learning paradigm has come from physics-informed machine learning. There, researchers have made great progress both in incorporating known physics into machine learning models, and elucidating new physics from raw data. As one example, the Sparse Identification of Nonlinear Dynamics (SINDy) architecture enables governing equations for dynamical systems to be discovered from data. Applying the insight that most physical equations possess only a small number of terms, SINDy uses regression to find the sparsest combination of a given set of basis functions that can adequately represent the data.

SINDy, being a form of regression, is technically not deep learning, and getting good results is highly dependent on the researcher choosing a coordinate system in which the dynamics permit sparse representation in the set of basis functions. Even when the coordinates and basis functions are well chosen, the magnitude of the enforced sparsity leads to a Pareto frontier of models that trade off number of terms in the final model with fit to the data.

Thus, while SINDy can point to a family of models that fit the data well, understanding which model is best requires understanding the physics behind the system, and how the math expresses that physics. That is, it requires an explanatory scientific understanding, going beyond the question of what math matches the data best.³ SINDy has also been incorporated into deep learning models, where first the input parameters are shrunk down into a reduced-dimensional encoding, and then SINDy is used to learn a model on the encoding. This allows the network to learn both a coordinate system that permits a sparse model and the dynamics on those coordinates at the same time. This however has the difficulty that the dimension of the encoding is a hyperparameter chosen by the researcher, and that, if even sparse dynamics are learned, it may not be clear what the coordinates actually represent. In the paper first demonstrating this method, two different models were learned for a pendulum system; in the general case, without prior knowledge of the proper dynamics and what the coordinates should represent, it would be difficult to decide between the two models.

SINDy is a relatively new method, and most of the papers written on it are proofs of concept, demonstrating that it can be applied to new types of known models. As of yet SINDy has not been used to solve any truly novel problems. However, because it is interpretable by design, it represents one of the best candidates for promoting the advance of science rather than engineering. At the same time, the interpretabilty comes at the cost of requiring much more background knowledge about the problem in question in order to obtain a solution that works, e.g. selecting the right coordinates and basis functions.

The obvious rebuttal here is that, compared to most physical systems, biological systems have orders of magnitude more interacting components, and the interactions themselves are more complex. Now that biological experiments are collecting terabytes of data at a time, do we have any other choice but to use deep learning models? Obviously humans simply do not have enough working memory to handle the billions or trillions of data points that are produced by modern experiments. And could it not be the case that biological systems are simply too complex to be understood by the kinds of laws that science has produced in the past? At some point, science runs up against the problem of computational irreducibility.

This question has merit, however I believe it speaks more to the indispensability of computational methods in science (Grey's third metaparadigm) as opposed to the necessity of data-driven deep learning methods. Data-driven methods work best when there is a massive combinatorial space (e.g. the space of all possible proteins), but only a very small percentage of that space (some embedded manifold) actually exists in practice. If there is enough of a pattern to be captured by a deep learning model, then that pattern or the rules governing it should be amenable to proper scientific modelling - refer back to the knot theory example. In fact the Gene Ontology is attempting to do just that for biology: it is a structured computational map of the state of knowledge in molecular biology. Green critiques the Ontology on the grounds that it is not clear how to transition from such a map to actionable control. Furthermore, any large-scale simulation derived from it would likely require enormous computational resources to produce useful results. In this light, the true benefit of deep learning models emerges from an engineering perspective: although these models are only statistical approximations of the true manifold, they may offer the most practical and efficient means of handling such complexity in real-world contexts.⁴

Computational fluid dynamics furnishes an illustrative example, since fluid experiments can collect quantities of data on par with omics experiments across a range of spatial and temporal scales. The field employs a variety of different models, from pure computational simulations, to deep learning models with embedded physics, to physics-free deep learning models. The equations governing fluid flow (the Navier-Stokes equations) are known, although it is extremely computationally expensive to simulate them for arbitrary geometries. If data can instead be collected from simulation or real-world experimentation, it is possible to train a deep learning model to capture the dynamics of the system much more cheaply than in a simulation. There are also hybrid models such as Physics-Informed Neural Networks (PINNs) that ensure that the trained model satisfies the known physics while also matching data. This enables models to be trained on less data, and to generalize better outside the data it was trained on. These hybrid models are currently the state of the art, however they are only possible because the physics of the system is already known. If physicists had not discovered the Navier-Stokes equations and had instead deemed the problem too difficult to solve due to the quantities of data and the time scales involved, they might have skipped simulation entirely. By proceeding directly to physics-free deep learning models, they would have settled for merely matching data rather than uncovering the underlying equations, which would have severely hamstrung progress in fluid dynamics. It would also have resulted in the creation of fluid models that are less physical, less robust to noise, and less able to generalize outside of their training data.

The biggest problem with data-driven research is that, as an instrumentalist metaparadigm, it cannot drive the emergence and elaboration of novel scientific paradigms - a key facet of scientific progress.⁵ This means that a machine-learning model is firmly embedded within a scientific paradigm - and cannot move past it. The variables it receives as input and the kinds of outputs it produces will be designed based on what variables the researcher believes are relevant. For instance, to return to Green's example, a model may be trained on raw sequencing reads matched to temporal and spatial data, with the goal of predicting future transcriptomic states. However, light environment is known to have significant effects on transcription, and outside of studies specifically looking at circadian rhythm, light environment is rarely controlled for or even mentioned in biomedical research.⁶ Thus if the light environment is not included in the data fed to the model, it will fail to accurately map reality due to missing an important degree of freedom. This is also not a problem that can be resolved within the model, or within the standard genetic and biochemical paradigm - it requires assimilating circadian and quantum biology. This problem is of course not specific to light environment: it could apply to any blind spot in our current scientific understanding. Such blind spots require the development of a novel scientific paradigm, which deep learning models, as engineering tools, cannot provide. If we discard genes as an abstraction when training our models, our models will not give us back any competing abstractions. They will just remain black boxes.

The danger of data-driven research as an ascendant metaparadigm is that we risk giving up actually understanding systems for an uninterpretable form of technocratic control, pulling levers to manipulate correlations we don't understand. Because deep learning methods are fundamentally limited in their ability to spur the development of explanatory theories, a shift in resources and talent toward data-driven approaches at the expense of traditional scientific methods is likely to hinder progress in fundamental science. Therefore, if machine learning is to be used for scientific applications, it must be applied in a way that elucidates, rather than obscures, causal mechanisms. The use of machine learning in dynamical systems research demonstrates that it is possible to use machine learning to potentially discover new physics, and use physics to improve the results of machine learning. This kind of reciprocal influence is the best path forward for the fourth metaparadigm. The danger posed by the bitter lesson is that it was learned from trying to bake human heuristics into ML models, rather than letting the model learn its own heuristics. When the goal is to engineer a tool, like an image classifier, a chatbot, or a self-driving car, the lesson applies. However when the goal is to advance science - that is the discovery not of heuristics but of the laws and mechanisms of nature - such approaches will only slow growth in the long term. The inverse of the bitter lesson, if you will.

---

References:

1. A Future History of Biomedical Progress. (2022, August 1). Markov Bio. https://markovbio.github.io/biomedical-progress/

2. Hey, A. J. G. (2009). The Fourth Paradigm: Data-intensive Scientific Discovery. Microsoft Research.

3. Davies, A., Juhász, A., Lackenby, M., & Tomasev, N. (2022). The signature and cusp geometry of hyperbolic knots (No. arXiv:2111.15323). arXiv. https://doi.org/10.48550/arXiv.2111.15323

4. Lackenby, M. (2023). Using machine learning to formulate mathematical conjectures. http://helper.ipam.ucla.edu/publications/map2023/map2023_17940.pdf

5. Brunton, S. L., Proctor, J. L., & Kutz, J. N. (2016). Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proceedings of the National Academy of Sciences, 113(15), 3932–3937. https://doi.org/10.1073/pnas.1517384113

6. Champion, K., Lusch, B., Kutz, J. N., & Brunton, S. L. (2019). Data-driven discovery of coordinates and governing equations. Proceedings of the National Academy of Sciences, 116(45), 22445–22451. https://doi.org/10.1073/pnas.1906995116

7. Alves, E. P. (2022). Data-driven discovery of reduced plasma physics models from fully kinetic simulations. Physical Review Research, 4(3). https://doi.org/10.1103/PhysRevResearch.4.033192

8. L, W., L, H., J, M., F, M., A, W., Ar, S., Da, B., Ar, W., Rj, L., & Tm, B. (2015). Colour as a signal for entraining the mammalian circadian clock. PubMed. https://pubmed.ncbi.nlm.nih.gov/25884537/

1. Here, feature engineering refers to humans deciding what aspects of the data to emphasize for the model. For instance, in older linguistics models, this involved incorporating structures like verb phrases and noun phrases; in contrast, LLMs operate without explicit linguistic knowledge yet significantly outperform these earlier models. Other examples include highlighting objects like pedestrians, cyclists, and other cars for self-driving car models, or selecting certain gene counts for biological models rather than providing raw sequencing data. Other ways of embedding knowledge into models include providing custom scoring functions for chess engines, or preprocessing images to detect edges and textures in image classification.

2. Saliency analysis of hyperbolic invariants predicting knot signature, from Using machine learning to formulate mathematical conjectures, Lackenby, M. (2023).

3. The danger here, or with any model that discovers equations that match data, is that the understanding never evolves past the existence of the equation. In that case, matching the data with a function of three parameters is scarcely better than matching the data with a neural-network based function of 3 billion parameters. The benefit of the low-dimensional model to the advance of fundamental physics is that it is easier to link the discovered equation with the actual mechanics of the system in question.

4. The caveat being that ML models are often extremely inefficient in the quantities of data required, although once they are trained they require vastly less computational resources than simulations in order to produce results.

5. See Conjectures and Refutations, chapter 3 section 5:

"We may sometimes be disappointed to find that the range of applicability of an instrument is smaller than we expected at first; but this does not make us discard the instrument qua instrument—whether it is a theory or anything else. On the other hand a disappointment of this kind means that we have obtained new information through refuting a theory—that theory which implied that the instrument was applicable over a wider range.

Instruments, even theories in so far as they are instruments, cannot be refuted, as we have seen. The instrumentalist interpretation will therefore be unable to account for real tests, which are attempted refutations, and will not get beyond the assertion that different theories have different ranges of application. But then it cannot possibly account for scientific progress."

6. Often where it is mentioned it is limited to the periodicity of the day-night cycle, neglecting information like spectral composition and timing, both of which affect circadian systems in mammals. Colour as a signal for entraining the mammalian circadian clock